УМОВА: Тиск на вільну поверхню рідини атмосферний

\[p_{0} =p_{a} =101325\; Па\]

діаметр трубопроводу

\[D=100\; мм \]

довжина нового сталевого трубопроводу

\[L=75\; м \]

еквівалентна шорсткість нової сталевої труби,Табличне значення

\[ {\Delta _{екв}} = 0.02\;мм\]

висота стовпа води

\[H=15 м\]

ЗАВДАННЯ. Розрахувати втрати напору (місцеві й по довжині):
- втрати напору по довжині \[\sum h_{l} \]
- втрати напору місцеві \[\sum h_{м} \]
- побудувати напірну і п’єзометричну лінії.

Розрахунок задачі

Розрахунок втрат напору за формулами:

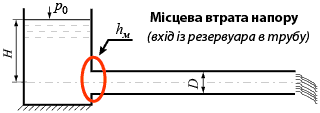
місцеві втрати напору за формулою \[h_{м} =\zeta \frac{V^{2} }{2g} \]

втрати напору по довжині за формулою Дарсі-Вейсбаха \[{h_l} = \lambda \frac{l}{D}\frac{{{V^2}}}{{2g}}\]

Призначаємо перерізи:

переріз 1-1 по вільній поверхні рідини та переріз 2-2 на виході із труби

Рівняння Д.Бернуллі в загальному вигляді:

\[{z_1} + \frac{{{p_1}}}{{\rho g}} + \frac{{\alpha V_1^2}}{{2g}} = {z_2} + \frac{{{p_2}}}{{\rho g}} + \frac{{\alpha V_2^2}}{{2g}} + \sum {\lambda \frac {l}{D}\frac{{\alpha V_2^2}}{{2g}}} + \sum {\zeta \frac{{\alpha V_2^2}}{{2g}}} \]

Рівняння Д.Бернуллі для перерізів 1-1 та 2-2:

\[{z_1} + \frac{{{p_a}}}{{\rho g}} + \frac{{V_1^2}}{{2g}} = {z_2} + \frac{{{p_a}}}{{\rho g}} + \frac{{V_2^2}}{{2g}} + \lambda \frac{l}{D}\frac{{V_2^2}}{{2g}} + {\zeta _{вх}}\frac{{V_2^2}}{{2g}}\]

Аналіз рівняння Д.Бернуллі для перерізів 1-1 та 2-2:

\[{z_1} = H,\;{V_1} = 0,\;{z_2} = 0\]

Рівняння Д.Бернуллі для перерізів 1-1 та 2-2:

\[H = \frac{{V_2^2}}{{2g}} + \lambda \frac{l}{D}\frac{{V_2^2}}{{2g}} + {\zeta _{вх}}\frac{{V_2^2}}{{2g}}\]

Табличне значення коефіцієнта місцевого опору

\[{\zeta _{вх}} = 0.5\]

---

ЕТАП 1. Гідравлічний коефіцієнт тертя у першому наближенні визначаєтся як для квадратичної області за формулою

\[\lambda = 0.11 \cdot {\left( {\frac{{{\Delta _{екв}}}}{D}} \right)^{0.25}}\]

Табличне значення еквівалентної шорсткості для новіх сталевих труб

\[\;{\Delta _{екв}} = 0.02\;мм\]

Рівняння Д.Бернуллі для перерізів 1-1 та 2-2:

\[H = \frac{{V_2^2}}{{2g}}\left( {1 + \lambda \frac{l}{D} + {\zeta _{вх}}} \right)\] \[{V_2} = \sqrt {\frac{{2gH}}{{\left( {1 + \lambda \frac{l}{D} + {\zeta _{вх}}} \right)}}} \]

\[\lambda = 0.11 \cdot {\left( {\frac{{0.02}}{{100}}} \right)^{0.25}} = 0.0131\]

\[\;{V_2} = \sqrt {\frac{{2 \cdot 9.81 \cdot 15}}{{\left( {1 + 0.0131 \cdot \frac{{75}}{{0.1}} + 0.5} \right)}}} = 5.1\; \left( { м }/{ с } \right)\]

(кінематична в'язкість води при температурі 20 С, Табличне значення

\[\nu = 1.01\cdot 10^{-6} \frac{м^{2}}{с} \]

Число Рейнольдса Re

\[{\mathop{\rm Re}\nolimits} = \frac{{VD}}{\nu } = \frac{{5.1*0.1}}{{0.000001}} = 505037\]

Визначаємо область гідравлічних опорів

\[{\mathop{\rm Re}\nolimits} \frac{{{\Delta _{ekv}}}}{D} = \frac{{505037 \cdot 0.00002}}{{0.1}} = 101.0\]

Отримано перехідну область гідравлічних опорів

\[10 < {\mathop{\rm Re}\nolimits} \frac{{{\Delta _{ekv}}}}{D} < 500\]

---

ЕТАП 2. Уточнюємо значення гідравлічного коеціфієнту тертя для перехідної зони

Алгоритм розрахунку коефіцієнте гідравлічного тертя Схема

\[\lambda = 0.11 \cdot {\left( {\frac{{{\Delta _{ekv}}}}{D} + \frac{{68}}{{{\mathop{\rm Re}\nolimits} }}} \right)^{0.25}}\]

\[\lambda = 0.11 \cdot {\left( {\frac{{{\Delta _{ekv}}}}{D} + \frac{{68}}{{{\mathop{\rm Re}\nolimits} }}} \right)^{0.25}} = 0.01487\]

Уточнюємо значення швидкості

\[{V_2} = \sqrt {\frac{{2 \cdot 9.81 \cdot 15}}{{\left( {1 + 0.01487 \cdot \frac{{75}}{{0.1}} + 0.5} \right)}}} = 4.82\; \left( { м }/{ с } \right)\]

Швидкісний напір

\[\frac{{V_2^2}}{{2g}} = \frac{{{{\left( {4.82} \right)}^2}}}{{2 \cdot 9.81}} = 1.1849\; м\]

Втрати напору по довжині

\[{h_l} = \lambda \frac{l}{D}\frac{{V_2^2}}{{2g}} = 0.01487\frac{{75}}{{0.1}}\frac{{{{\left( {4.82} \right)}^2}}}{{2 \cdot 9.81}} = 13.22\; \left( { м }\right)\]

Втрати напору місцеві

\[{h_m} = {\zeta _{vh}}\frac{{V_2^2}}{{2g}} = 0.5\frac{{{{\left( {4.82} \right)}^2}}}{{2 \cdot 9.81}} = 0.5925\; \left( { м }\right)\]

Перевірка розрахунків втрати напорів

\[H = \frac{{{V^2}}}{{2g}} + {h_l} + {h_m} = 1.1849 + 13.2225 + 0.5924 = 15\; \left( { м }\right)\]

Побудувати напірну і п’єзометричну лінії

П’єзометрична лінія (потенційна енергія)

Напірна лінія (повна енергія потоку)

---

Рівняння Д.Бернуллі для в'язкої рідини
ON-LINE розрахунок (Варіанти типових задач)