D:\jknuba_2025_spring\jknuba_MSC\jknuba_MSC_DOC\
jknuba_MSC_Job3_All.wxmx

kill - Removes all bindings (value, function, array, or rule) from the arguments a_1, …, a_n. An argument a_k may be a symbol or a single array element.
(%i1) kill(all);

\[\]\[\tag{%o0} \ensuremath{\mathrm{done}}\]

Package stats contains a set of classical statistical inference and hypothesis testing procedures.
Package stats loads packages descriptive, distrib
Package descriptive contains a set of functions for making descriptive statistical computations and graphing.
(%i1) load("stats")$
This normally means that a list, a set or something else that consists of more than one element was expected.
(%i2) p:[59.39762397483823,    12.68700015685627,    31.35538411535527,    23.1036037153536,    16.39552698454976,    27.01157697689639,    39.8173028014986,    54.71782259683489,    32.86331390184777,    44.10002967620344,    2.365565533494923,    40.64433869221747,    64.59254476151632,    2.703301000039238,    41.12065030882908,    38.55489179860347,    42.55275479744299,    30.59619381218819,    3.375030988193638,    0.1513122243954068,    20.51450025858425,   55.91491920591274,    2.734255975155692,    55.16354628521058,    15.14354144838837,    44.92242265044037,    39.75112753258765,    56.62421750522258,    9.863393407881814,    41.35089981759533,    42.80463303851646,    38.39042860902299,    30.44905471801171,    50.10507869829214,    45.79592830044311,    33.52522232509477,    48.65922943483395,    20.80334721705067,    29.42590881770415,    8.333780516619887,    43.7196955856165,    1.063999940204406,    50.86120105609081,    17.11882275390031,    10.58429445907518,    60.03274138897483,    5.351089442351305,    7.896425257058851,    58.70439635154142,    42.06021218741804,    55.3367642799664,    35.37948530261435,    2.799704152460334,    43.16506440140017,    59.17919419751087,    62.69640197149587,    6.44243467651085,    12.89419376857005,    18.64249519577364,    52.12195830133088,    53.53279479251758,    10.65037878149241,    35.30942715378566,    18.33293003081024,    18.48059931632189,    38.90586123842466,    26.25131184483497,    3.318332682217242,    46.75062151347198,    43.72625516704196,    63.9909979311192,    46.03068974336779,    7.193358353151108,    29.65708334839154,    52.40237751210758,    36.78245806593392,    21.06493261212433,    48.87876636548086,    23.72632507601132,    41.25105453851204,    56.59427438532665,    37.42010498415079,    5.628126184621783,    35.33261368945548,    43.80297624358005,    35.22107942536941,    61.40171930123801,    9.053453438177984,    16.03950951478958,    7.377139957815818,    41.47586339047343,    59.46353293109683,    13.42941713508699,    38.33555283152583,    32.64690943784151,    37.68425793066372,    35.36199757913382,    23.6617856124797,39.42508294452147,    37.82554332062914];

\[\]\[\tag{%o2} \]

length - Returns (by default) the number of parts in the external (displayed) form of expr. For lists this is the number of elements, ...
(%i3) length (p);

\[\]\[\tag{%o3} 100\]

Figure 1:D:\jknuba_2025_spring\jknuba_MSC\_j_Stat_Ebook\jknuba_MSC_Job3\Normal_distribution_pdf.jpg
Diagram
histogram - Constructs and displays a histogram from a data sample. Data must be stored as a list of numbers, ...
(%i4) histogram ( p, nclasses = 10, title = "Histogram", xlabel = "Values", ylabel = "Count of values", fill_color = red
    , fill_density = 0.4);

\[\]\[\tag{%o4} \left[ \mathop{gr2d}\left( \ensuremath{\mathrm{bars}}\right) \right] \]

Function: smin
smin (list)
smin (matrix)

This is the minimum value of the sample list.
Figure 2:D:\jknuba_2025_spring\jknuba_MSC\_j_Stat_Ebook\jknuba_MSC_Job3\jknuba_Job3_histogram_pic.svg
Diagram
(%i5) smin(p);

\[\]\[\tag{%o5} 0.1513122243954068\]

Function: smax
smax (list)
smax (matrix)

This is the maximum value of the sample list.
(%i6) smax (p);

\[\]\[\tag{%o6} 64.59254476151632\]

This is the sample mean, defined as

n
====
_ 1 \
x = - > x
n / i
====
i = 1
(%i7) mean(p);

\[\]\[\tag{%o7} 32.77849275554686\]

range - The range is the difference between the extreme values.
(%i8) range(p);

\[\]\[\tag{%o8} 64.44123253712091\]

Function: quantile
quantile (list, p)
quantile (matrix, p)

This is the p-quantile, with p a number in [0,1], of the sample list. Although there are several definitions for the sample quantile (Hyndman, R. J., Fan, Y. (1996) Sample quantiles in statistical packages. American Statistician, 50, 361-365), the one based on linear interpolation is implemented in package descriptive
(%i15) quantile (p, 0);quantile (p, 1/4);quantile (p, 2/4);quantile (p, 3/4);quantile (p, 4/4);smin(p);smax(p);

\[\]\[\tag{%o9} 0.1513122243954068\]

\[\]\[\tag{%o10} 16.93799881156267\]

\[\]\[\tag{%o11} 36.08097168427413\]

\[\]\[\tag{%o12} 45.140799062941056\]

\[\]\[\tag{%o13} 64.59254476151632\]

\[\]\[\tag{%o14} 0.1513122243954068\]

\[\]\[\tag{%o15} 64.59254476151632\]

Function: qrange
qrange (list)
qrange (matrix)

The interquartilic range is the difference between the third and first quartiles, quantile(list,3/4) - quantile(list,1/4),
(%i16) qrange (p);

\[\]\[\tag{%o16} 28.202800251378385\]

(%i17) quantile (p, 3/4)−quantile (p, 1/4);

\[\]\[\tag{%o17} 28.202800251378385\]

median - Once the sample is ordered, if the sample size is odd the median is the central value, otherwise it is the mean of the two central values.
(%i18) median(p);

\[\]\[\tag{%o18} 36.08097168427413\]

Function: mean_deviation
mean_deviation (list)
mean_deviation (matrix)

The mean deviation, defined as

n
====
1 \ _
- > |x - x|
n / i
====
i = 1
(%i19) mean_deviation (p);

\[\]\[\tag{%o19} 15.463157152994444\]

Function: var
var (list)
var (matrix)

This is the sample variance, defined as

n
====
2 1 \ _ 2
s = - > (x - x)
n / i
====
i = 1

Function: median_deviation
median_deviation (list)
median_deviation (matrix)

The median deviation, defined as

n
====
1 \
- > |x - med|
n / i
====
i = 1

where med is the median of list.
(%i20) median_deviation (p);

\[\]\[\tag{%o20} 14.898134221983241\]

Function: skewness
skewness (list)
skewness (matrix)

The skewness coefficient, defined as

n
====
1 \ _ 3
---- > (x - x)
3 / i
n s ====
i = 1
Figure 3:D:\jknuba_2025_spring\jknuba_MSC\_j_Stat_Ebook\jknuba_MSC_Job3\jknuba_MSC_Job3_skewness.jpg
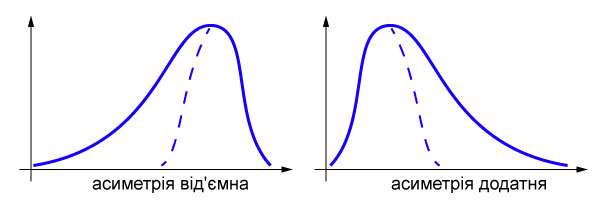
Diagram
(%i21) skewness (p);

\[\]\[\tag{%o21} \mathop{-}0.18190942734904172\]

(%i22) var(p);

\[\]\[\tag{%o22} 329.3280691729721\]

Function: var1
var1 (list)
var1 (matrix)

This is the sample variance, defined as

n
====
1 \ _ 2
--- > (x - x)
n-1 / i
====
i = 1
(%i23) var1(p);

\[\]\[\tag{%o23} 332.6546153262344\]

Function: std
std (list)
std (matrix)

This is the square root of the function var, the variance with denominator n.
(%i24) std (p);

\[\]\[\tag{%o24} 18.14739841335314\]

Function: std1
std1 (list)
std1 (matrix)

This is the square root of the function var1, the variance with denominator n−1.
(%i25) std1 (p);

\[\]\[\tag{%o25} 18.238821653994933\]

test_mean - This is the mean t-test. Argument x is a list or a column matrix containing an one dimensional sample.
(%i26) test_mean(p);

\[\]\[\tag{%o26} \begin{array}{c}"MEAN TEST"\\ \ensuremath{\mathrm{mean\_ estimate}}\mathop{=}32.77849275554686\\ \ensuremath{\mathrm{conf\_ level}}\mathop{=}0.95\\ \ensuremath{\mathrm{conf\_ interval}}\mathop{=}\left[ 29.159515991377067\mathop{,}36.397469519716644\right] \\ \ensuremath{\mathrm{method}}\mathop{=}"Exact t-test. Unknown variance."\\ \ensuremath{\mathrm{hypotheses}}\mathop{=}"H0: mean = 0 , H1: mean \neq 0"\\ \ensuremath{\mathrm{statistic}}\mathop{=}17.971825909250686\\ \ensuremath{\mathrm{distribution}}\mathop{=}\left[ {{\ensuremath{\mathrm{student}}}_t}\mathop{,}99\right] \\ {p_{\ensuremath{\mathrm{value}}}}\mathop{=}0.0\end{array}\]

(%i27) test_mean(p ,'conflevel=0.9, 'mean=32.77849275554686);

\[\]\[\tag{%o27} \begin{array}{c}"MEAN TEST"\\ \ensuremath{\mathrm{mean\_ estimate}}\mathop{=}32.77849275554686\\ \ensuremath{\mathrm{conf\_ level}}\mathop{=}0.9\\ \ensuremath{\mathrm{conf\_ interval}}\mathop{=}\left[ 29.75013545566007\mathop{,}35.80685005543364\right] \\ \ensuremath{\mathrm{method}}\mathop{=}"Exact t-test. Unknown variance."\\ \ensuremath{\mathrm{hypotheses}}\mathop{=}"H0: mean = 32.77849275554686 , H1: mean \neq 32.77849275554686"\\ \ensuremath{\mathrm{statistic}}\mathop{=}0.0\\ \ensuremath{\mathrm{distribution}}\mathop{=}\left[ {{\ensuremath{\mathrm{student}}}_t}\mathop{,}99\right] \\ {p_{\ensuremath{\mathrm{value}}}}\mathop{=}1.0\end{array}\]

(%i28) test_mean(p ,'conflevel=0.95, 'mean=32.77849275554686);

\[\]\[\tag{%o28} \begin{array}{c}"MEAN TEST"\\ \ensuremath{\mathrm{mean\_ estimate}}\mathop{=}32.77849275554686\\ \ensuremath{\mathrm{conf\_ level}}\mathop{=}0.95\\ \ensuremath{\mathrm{conf\_ interval}}\mathop{=}\left[ 29.159515991377067\mathop{,}36.397469519716644\right] \\ \ensuremath{\mathrm{method}}\mathop{=}"Exact t-test. Unknown variance."\\ \ensuremath{\mathrm{hypotheses}}\mathop{=}"H0: mean = 32.77849275554686 , H1: mean \neq 32.77849275554686"\\ \ensuremath{\mathrm{statistic}}\mathop{=}0.0\\ \ensuremath{\mathrm{distribution}}\mathop{=}\left[ {{\ensuremath{\mathrm{student}}}_t}\mathop{,}99\right] \\ {p_{\ensuremath{\mathrm{value}}}}\mathop{=}1.0\end{array}\]

Відповідь:
- оцінка форми гістограми;
- порівняти середнє, моду, медіану, коефіцієнт асиметрії
- показати довірчій інтервал.

Created with wxMaxima.

The source of this Maxima session can be downloaded here.